immokerop.blogg.se

Fortunately, it is not at all sensitive to deviations from this assumption, if the distributions of the two groups are the same (if both distributions are skewed to the right, for example). The t–test assumes that the observations within each group are normally distributed. The degrees of freedom for a t–test is the total number of observations in the groups minus 2, or n 1+n 2−2. The shape of the t-distribution, and thus the probability of getting a particular t s value, depends on the number of degrees of freedom. You calculate the probability of getting the observed t s value under the null hypothesis using the t-distribution. Thus t s gets larger as the means get farther apart, the variances get smaller, or the sample sizes increase. The denominator is the standard error of the difference in the means, which gets smaller as the sample variances decrease or the sample sizes increase. The test statistic, t s, is calculated using a formula that has the difference between the means in the numerator this makes t s get larger as the means get further apart. The statistical null hypothesis is that the means of the measurement variable are equal for the two categories. The nominal variable must have only two values, such as "male" and "female" or "treated" and "untreated." Null hypothesis Use the two-sample t–test when you have one nominal variable and one measurement variable, and you want to compare the mean values of the measurement variable. Student's t–test for two samples is mathematically identical to a one-way anova with two categories because comparing the means of two samples is such a common experimental design, and because the t–test is familiar to many more people than anova, I treat the two-sample t–test separately.

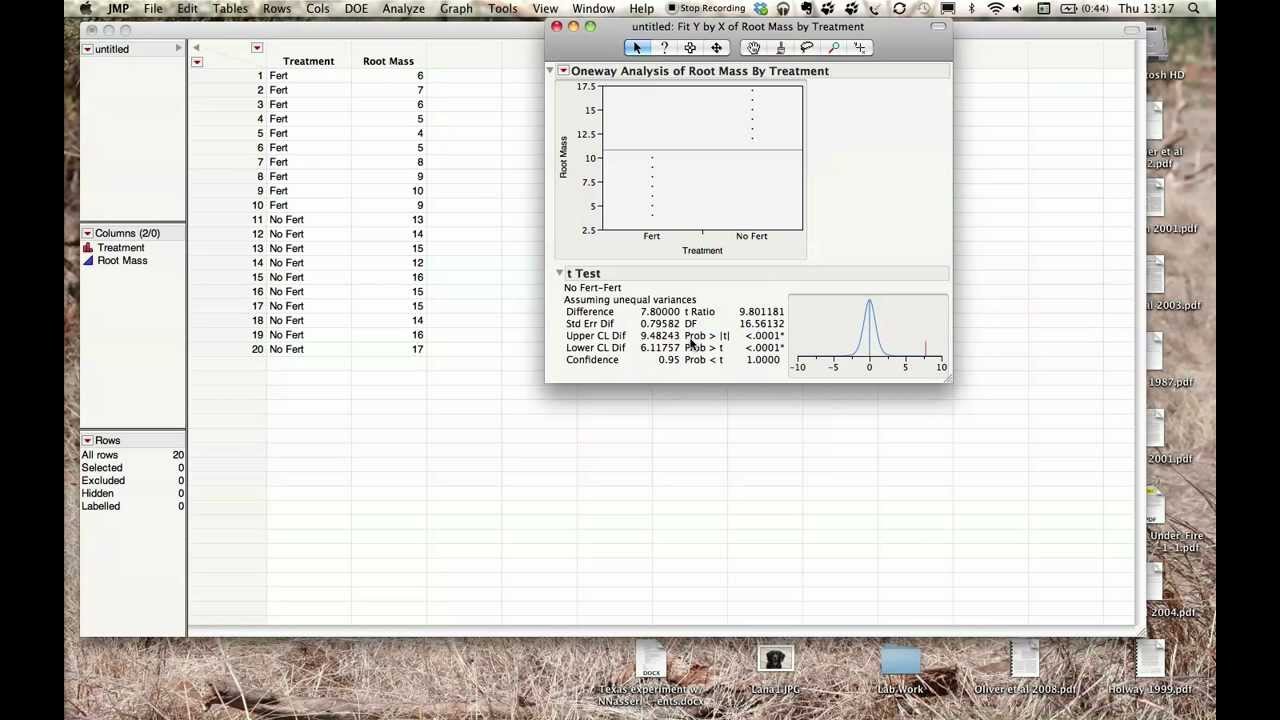
Other t–tests include the one-sample t–test, which compares a sample mean to a theoretical mean, and the paired t–test. One of the most common is Student's t–test for two samples. There are several statistical tests that use the t-distribution and can be called a t–test. It tests whether the means of the measurement variable are different in the two groups. Use Student's t–test for two samples when you have one measurement variable and one nominal variable, and the nominal variable has only two values.